Third Grade Math Worksheets
 Category: Review Math for 3rd Graders
Category: Review Math for 3rd Graders
Third-grade math instruction is focused on the following areas: developing an understanding of multiplication and division and strategies for multiplication and division within 100; developing an understanding of fractions, especially unit fractions (fractions with numerator 1); developing an understanding of the structure of rectangular arrays and of area; describing and analyzing two-dimensional shapes.
The best way to ensure your students fully grasp the math concepts they'll need to successfully progress in their education is to practice as much as possible. The worksheets, puzzles, games, and other resources available here are the perfect solution for parents and teachers who want to provide their third graders with the tools they need to understand and excel in third-grade math.
Free Third Grade Math Worksheets:(No Login)
New Math Worksheets for Third Graders Each Month
3rd Grade Math and Critical Thinking Worksheets
Math Assessments and Hybrid AI Learning:
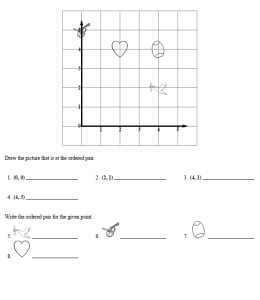
Place Value and Large Numbers
Numbers to 1,000 (easier)
Addition (easier)
Subtraction (easier)
Time and Clocks (easier)
Mental Math
Fractions Challenge
Whole Numbers and Place Value
Addition
Multiply 6,7
Multiply 8,9
Introduction to Money
Clocks and Time
Geometry Challenge
Subtraction
Money Challenge (difficult)
Multiplication
Division (easier)
Fractions (easier)
Division
Fractions
Math Workbooks for Third Graders following Common Core Standards:
Chapter 1: Numbers to 10,000
Place Value (challenge pages)
Chapter 2: Mental Math and Estimation
Using Bar Models: Addition and Subtraction
Cumulative Review (Chapters 1-2)
Chapter 3: Addition Up to 10,000
Chapter 4: Subtraction Up to 10,000
Multiplication and Division (Introduction)
Cumulative Review (Chapters 3-4)
Sept/Oct Math Review (3rd grade)
Math Review of Chapters 1-4 (No Sept/Oct Pages)
Chapter 5: Using Bar Models: Addition and Subtraction
Chapter 6: Multiplication and Mental Math
Tables and Line Graphs
Cumulative Review (Chapters 5-6)
Mid-Year Math Review
Chapter 7: Multiplication (with one factor being larger than one digit)
Nov/Dec Math Review
Chapter 8: Division
Number Theory (challenge pages)
Multiplication and Division (challenge pages)
Fractions and Mixed Numbers (challenge pages)
Chapter 9: Using a Bar Model: Multiplication and Division
Third Quarter Review (Chapters 1-9)
Chapter 10: Money
Chapter 11: Metric Length, Mass, and Volume
Chapter 12: Real-World Problems: Measurement
Chapter 13: Bar Graphs and Line Plots
Chapter 14: Fractions
Chapter 15: Customary Length, Weight, and Capacity
Chapter 16: Time and Temperature
Chapter 17: Angles and Lines
Chapter 18: Two-Dimensional Shapes
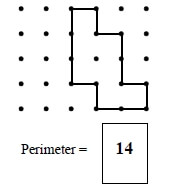
Chapter 19: Area and Perimeter
Geometry Workbooks for 3rd grade:
Geometry Chapter 1: Polygons
-

Math Assessments and Hybrid AI Learning (3rd grade)
-

This Week's Math Review Book for Third Graders - Updated Each Week
-

Third Grade Math Minutes
-

Math Problem of the day - Robot helps kids answer a challenging question.
-

3rd grade Monthly Math Challenge Book
-

Third Grade Math Puzzle Worksheets
-

Third Grade Mad Minute Timed Math Drill Worksheets
-

Third Grade Coding for Kids with Math
-

This Week's Reading and Math Book for Third Graders
-

Mental Math Practice Problems
-

Third Grade Math Assessment Practice PDF Pages
-

Addition Mixed Math PDF Book
-

Assessment Mixed Math PDF Book
-
Data Mixed Math PDF Book
-

Division Mixed Math PDF Book
-

Enrichment Mixed Math PDF Book
-
Fractions Mixed Math PDF Book
-
Mad Minute Timed Math Drills Mixed Math PDF Book
-

Math Challenges - Puzzles and Brain Teasers Mixed Math PDF Book
-
Math Facts Practice Mixed Math PDF Book
-

Math Minutes Mixed Math PDF Book
-

Measurement Mixed Math PDF Book
-
Mental Math Mixed Math PDF Book
-

Money Math Mixed Math PDF Book
-

Multiplication Mixed Math PDF Book
-
Number Sense Mixed Math PDF Book
-

Patterns Mixed Math PDF Book
-
Place Value Mixed Math PDF Book
-

Read and Math Mixed Math PDF Book
-

Rounding Mixed Math PDF Book
-

Subtraction Mixed Math PDF Book
-

Word Problems Mixed Math PDF Book
Third-Grade Math Curriculum: What Students Will Learn
In third grade, students will be expected to know addition, subtraction, multiplication, and division facts and use them in equations and word problems. Third-graders should know how to place values for numbers up to six digits, read and write large numbers, and round and compare numbers. They should understand equivalent fractions and be able to compare fractions.
In addition, third-graders should know how to round decimals to the one-hundredth place, recognize and write patterns, add four-digit numbers, and do mental addition and subtraction. They should use number lines, know how to subtract with regrouping, read and make graphs, and recognize two-dimensional shapes.
That may seem like a lot of math facts for a third-grader to master! The major concepts of third-grade math curriculum are number theory and systems, algebraic thinking, geometrical figures and objects, measurement of length, weight, time, and temperature, probability, and data analysis. The path to mastering math can be fraught with challenges, and third grade can be especially challenging, as many new and complicated math theories are introduced.